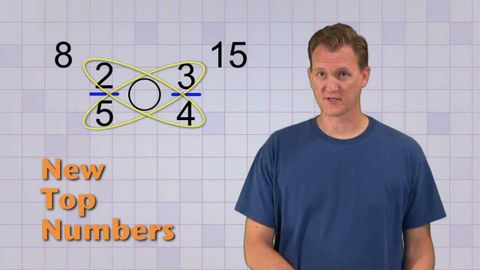
數學反常學 - 比較分數 (Math Antics - Comparing Fractions)
Yassion Liu 發佈於 2021 年 01 月 14 日  沒有此條件下的單字
沒有此條件下的單字US /ˈpræktɪs/
・
UK /'præktɪs/
- n.(醫生;律師等的)業務;工作;練習;慣例
- v.t./i.(醫生;律師等)開業;實踐;練習;操練;實踐
- n. (c./u.)範本;典範;圖案;花樣;模式;方式;規律;紙樣
- v.t.仿造;用圖案裝飾
- adj.美麗的,可愛的;漂亮的
- adv.十分;相當
- v.t.美化
- n.漂亮的東西或人
- v.t.詭計:騙局:花招;惡作劇;戲弄
- n. (c./u.)戲法;竅門;訣竅;把戲;特技
- adj.虛弱的;欺詐的