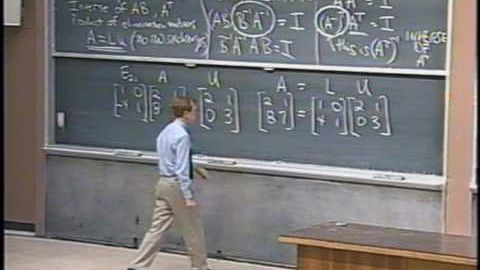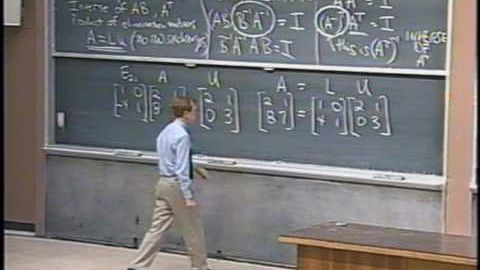字幕列表影片播放

    字幕與單字

    00
    收藏
    影片單字

    sort

    US /sɔrt/

    ・

    UK /sɔ:t/

    • v.t.整理，整頓；分類
    • n.種類
    A1 初級多益初級英檢
    更多
    decent

    US /ˈdisənt/

    ・

    UK /ˈdi:snt/

    • adj.正派的； 得體的；正派的；慷慨的；穿著得體的；相當可觀的
    B1 中級高級英檢
    更多
    practical

    US /ˈpræktɪkəl/

    ・

    UK /ˈpræktɪkl/

    • adj.實際的；實用的；實際的；務實的
    • n.實作；注重實踐的人
    A2 初級多益中級英檢
    更多
    position

    US /pəˈzɪʃən/

    ・

    UK /pəˈzɪʃn/

    • n. (c./u.)態度，觀點；位置；(團隊運動中個人所處的)位置；職位；處境；優勢
    • v.t.定位；放置
    A1 初級多益初級英檢
    更多
    使用能量
    解鎖所有單字
    解鎖發音、解釋及篩選功能
    energy point vocabulary