字幕與單字
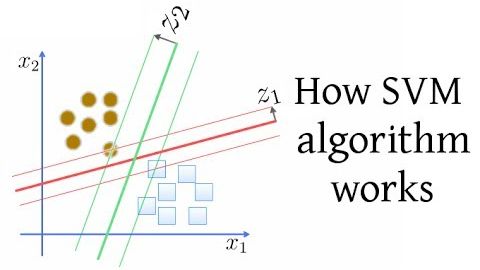
SVM(支持向量機)算法的工作原理 (How SVM (Support Vector Machine) algorithm works)
00
dœm 發佈於 2021 年 01 月 14 日收藏
影片單字
split
US /splɪt/
・
UK /splɪt/
- adj.分裂的;分離的;裂開的;(比賽)打成平局
- v.t./i.被劈開;被切開;撕裂;使分離;使不團結;分裂:劈開;(平均)分配
- n. (c./u.)分裂;分割;分裂
A2 初級中級英檢
更多 使用能量
解鎖所有單字
解鎖發音、解釋及篩選功能
