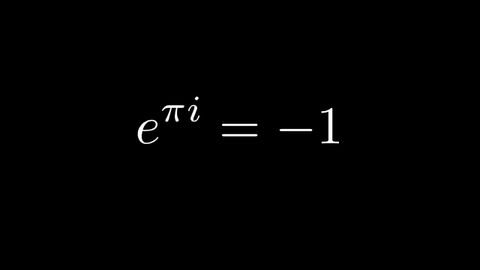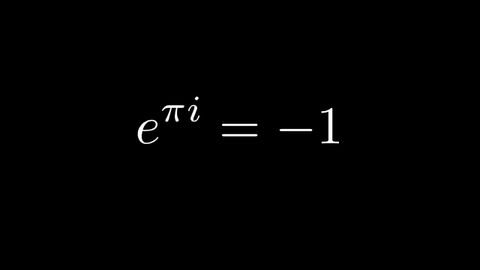理解e到pi i (Understanding e to the pi i)
jeffrey 發佈於 2021 年 01 月 14 日  沒有此條件下的單字
沒有此條件下的單字- v.t./i.伸展(肢體等);拉長
- n.伸展;一段路程、區域;物品連續排列;一段時間;階段
US /ɪkˈsprɛʃən/
・
UK /ɪk'spreʃn/
- n. (c./u.)表達;措辭;表情;表達式;表現;表現
US /saɪməlˈtenɪəslɪ/
・
UK /ˌsɪməl'teɪnɪəslɪ/
- n. (c./u.)條件;條款;期間;期限;學期;術語;關係;項;妊娠期;任期
- v.t.命名