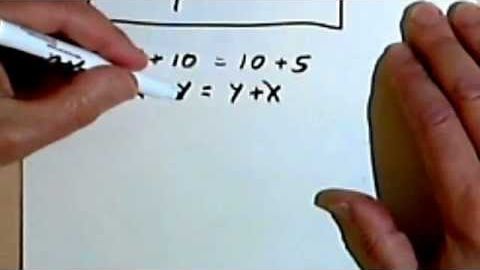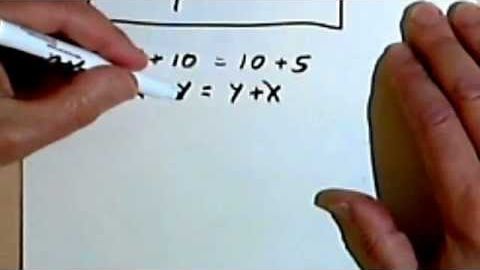字幕列表影片播放

    字幕與單字

    00
    收藏
    影片單字

    obvious

    US /ˈɑbviəs/

    ・

    UK /ˈɒbviəs/

    • adj.明顯的；顯而易見的 ；顯而易見的；明目張膽的
    A2 初級多益中級英檢
    更多
    basically

    US /ˈbesɪkəli,-kli/

    ・

    UK /ˈbeɪsɪkli/

    • adv.根本上 ； 基本上；實質上；簡單地說
    A2 初級高級英檢
    更多
    associate

    US /əˈsoʊʃiˌeɪt/

    ・

    UK /ə'səʊʃɪeɪt/

    • n. (c.)同事；合夥人
    • v.t./i.有關聯的；關聯
    • adj.副手
    B1 中級多益中級英檢
    更多
    positive

    US /ˈpɑzɪtɪv/

    ・

    UK /ˈpɒzətɪv/

    • adj.積極的；建設性的；確定的；正極的；積極的；有利的；陽性的；樂觀的；正數的；正像的
    • n.正片
    A2 初級初級英檢
    更多
    使用能量
    解鎖所有單字
    解鎖發音、解釋及篩選功能
    energy point vocabulary