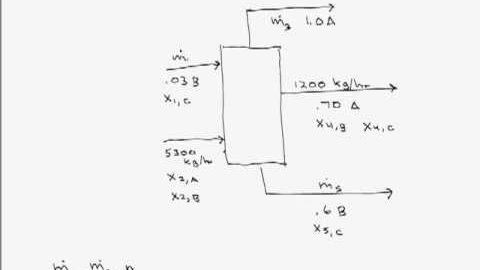
單一組織、部門的自由度分析 (Degree of Freedom Analysis on a Single Unit)
Jack 發佈於 2021 年 01 月 14 日  沒有此條件下的單字
沒有此條件下的單字- v.t./i.出現;估計;我認為〜;認為
- n.身影;(計算過的)數量;肖像;圖;形狀;人物;名人;人影;數字
- v.i.到達、到來;來、寄送到;來
- v.t./i.來 ; 去 ; 到 ; 赴
US /kəmˈpliːtli/
・
UK /kəmˈpli:tli/
- n. (c./u.)休息時間;靜止;剩餘部分;支撐物;休止符
- v.t./i.使休息;使安息;倚靠;使休息;放置;歸於