字幕列表影片播放

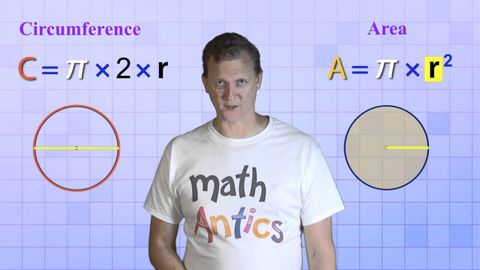
    字幕與單字

    00
    收藏
    影片單字

    common

    US /ˈkɑmən/

    ・

    UK /'kɒmən/

    • n. (c./u.)公有地；公共用地；廣場
    • adj.共用的；常見的；普通的；普遍的；粗俗的；普通名詞
    A1 初級初級英檢
    更多
    pretty

    US /ˈprɪti/

    ・

    UK /'prɪtɪ/

    • adj.美麗的，可愛的；漂亮的
    • adv.十分；相當
    • v.t.美化
    • n.漂亮的東西或人
    A1 初級多益初級英檢
    更多
    world

    US /wɜrld /

    ・

    UK /wɜ:ld/

    • n. (c./u.)世界；地球；世界；世界；宇宙；領域
    A1 初級初級英檢
    更多
    start

    US /stɑrt/

    ・

    UK /stɑ:t/

    • n. (c./u.)開端；(某事的)開始；開始；出發點；突然一驚；嚇一跳
    • v.t./i.開始；首次(做某事)
    • v.t.使開始運轉；啟動
    A1 初級初級英檢
    更多
    使用能量
    解鎖所有單字
    解鎖發音、解釋及篩選功能
    energy point vocabulary