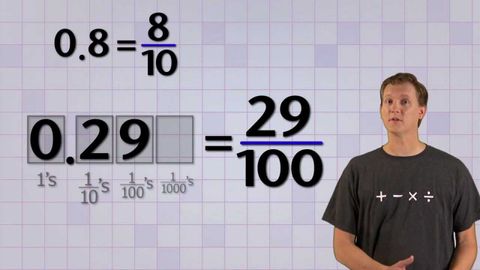
字幕與單字
數學反常--10基數的換算 (Math Antics - Converting Base-10 Fractions)
00
Yassion Liu 發佈於 2021 年 01 月 14 日收藏
影片單字
time
US /taɪm/
・
UK /taɪm/
- n. (u.)節拍;(準確的)時間;時間(多寡);(經歷的)一段時光;(經歷的)時光;時代;時期;時間;時刻;時候
- v.t.測量(節拍);為...計算時機;計時;測量時間;使適時;安排...的時間
A1 初級多益初級英檢
更多 使用能量
解鎖所有單字
解鎖發音、解釋及篩選功能
