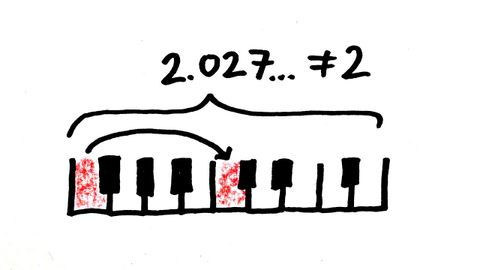
為什麼不可能給鋼琴調音? (Why It's Impossible to Tune a Piano)
 沒有此條件下的單字
沒有此條件下的單字- n. (c./u.)大小;規模;魚鱗;比例;等級;標尺
- v.t./i.測量;攀登;魚鱗
US /ˈslaɪtli/
・
UK /ˈslaɪtli/
- adj.可靠的;熟睡(的);酣睡(的);無損傷的;完好的;健全的;明智的
- n. (c./u.)音樂特色;音樂風格;聲音,聲響
- v.i.聽起來,聽起來好像;發出聲響,發聲
- v.t.(使)發聲;(使)作響
US /ˈmedʒɚ/
・
UK /'meɪdʒə(r)/
- n. (c.)陸軍少校;主要專業;;成年人
- adj.大聯盟;最重要的;一個主要;較大的;主要的;大調的
- v.i.到主要