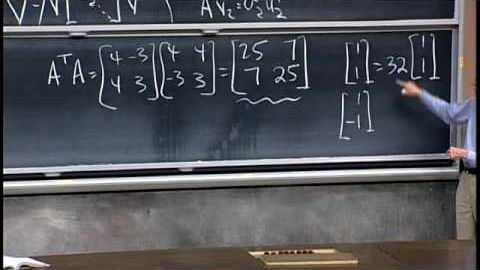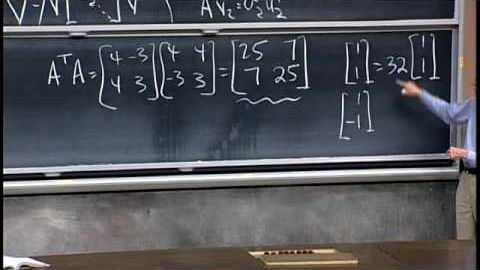Lec 29 | MIT 18.06 Linear Algebra, Spring 2005 (Lec 29 | MIT 18.06 Linear Algebra, Spring 2005)
gtasa2009 發佈於 2021 年 01 月 14 日  沒有此條件下的單字
沒有此條件下的單字US /ˈpɑzɪtɪv/
・
UK /ˈpɒzətɪv/
- adj.積極的;建設性的;確定的;正極的;積極的;有利的;陽性的;樂觀的;正數的;正像的
- n.正片
- n. (c./u.)(停車場等)空間;(可使用的)空間;宇宙,太空;空格,字距
- v.t.留出空白,留間隔
- n. (c./u.)根源;根源;祖先;(數學方程式的)根;根;(牙齒;頭髮等的)根;根部;字根;原形
- v.t.生根;(動物)挖掘;翻找;使固定
- n. (c./u.)正方形;面積;廣場
- adj.正直的;公正的;平方米
- adv.直截了當的;斷然的
- v.t.調整,改正;二次冪,平方;使挺直;使平正