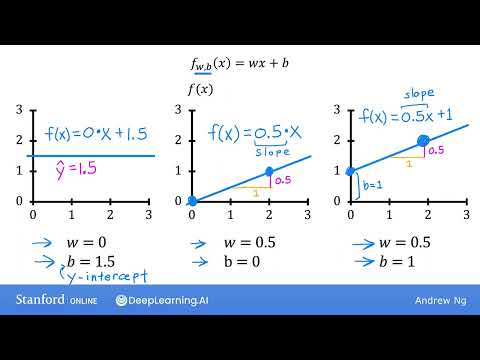
#11 機器學習專業【課程 1,第 1 周,第 3 課 (#11 Machine Learning Specialization [Course 1, Week 1, Lesson 3])
 沒有此條件下的單字
沒有此條件下的單字US /ɛnˈtaɪr/
・
UK /ɪn'taɪə(r)/
- adj.全體的 ; 完全的;未分割的;全緣的 (植物學)
US /ɪˈvɛntʃuəli/
・
UK /ɪˈventʃuəli/
US /ˈkɑnstənt/
・
UK /'kɒnstənt/
US /ɪkˈsprɛʃən/
・
UK /ɪk'spreʃn/
- n. (c./u.)表達;措辭;表情;表達式;表現;表現