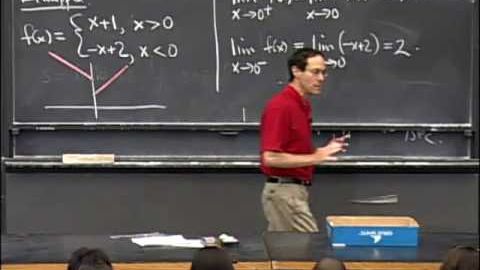
字幕與單字
講座 2 | MIT 18.01 單變量微積分,2007 年秋季(Lec 2 | MIT 18.01 Single Variable Calculus, Fall 2007)
00
lokcm7 發佈於 2024 年 04 月 11 日收藏
影片單字
average
US /ˈævərɪdʒ, ˈævrɪdʒ/
・
UK /'ævərɪdʒ/
- n. (c./u.)平均
- v.t.算出...的平均數
- adj.平均的;一般的,通常的;中等的
A2 初級多益中級英檢
更多 使用能量
解鎖所有單字
解鎖發音、解釋及篩選功能
