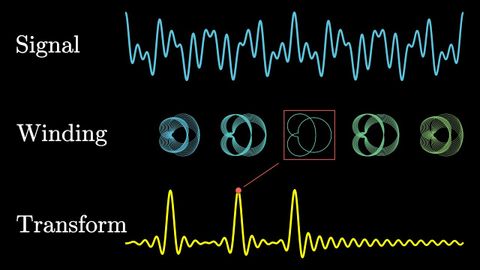
可視化的傅里葉變換(But what is the Fourier Transform? A visual introduction.)
Sujuku 發佈於 2022 年 11 月 16 日  沒有此條件下的單字
沒有此條件下的單字US /ˈkɑnˌtɛkst/
・
UK /ˈkɒntekst/
- n. (c./u.)上下文 ; 背景 ; 來龍去脈;背景;環境;語境
US /ɪkˈsprɛʃən/
・
UK /ɪk'spreʃn/
- n. (c./u.)表達;措辭;表情;表達式;表現;表現
- n. (c./u.)大小;規模;魚鱗;比例;等級;標尺
- v.t./i.測量;攀登;魚鱗
US /ˈnɛɡətɪv/
・
UK /'neɡətɪv/
- n.負電極的;否定詞;否定句;底片
- adj.消極的;負的;負面的;否定的;陰性的;負電的