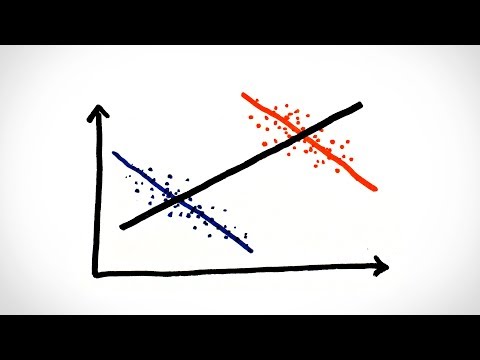
Simpson's Paradox
Summer 發佈於 2021 年 10 月 18 日  沒有此條件下的單字
沒有此條件下的單字US /ˈkɑnˌtɛkst/
・
UK /ˈkɒntekst/
- n. (c./u.)上下文 ; 背景 ; 來龍去脈;背景;環境;語境
US /ˌsɪtʃuˈeʃən/
・
UK /ˌsɪtʃuˈeɪʃn/
US /ˈpræktɪs/
・
UK /'præktɪs/
- n.(醫生;律師等的)業務;工作;練習;慣例
- v.t./i.(醫生;律師等)開業;實踐;練習;操練;實踐
US /ɪmˈpruv/
・
UK /ɪm'pru:v/