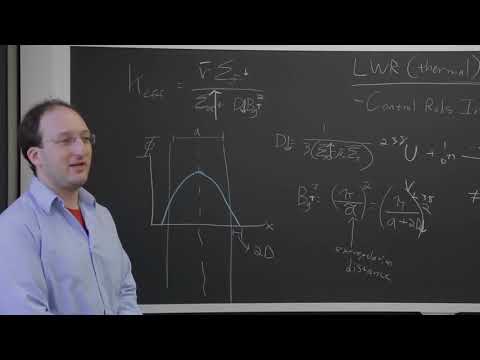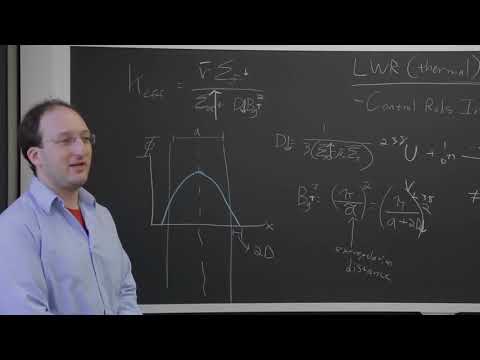24.瞬態、反饋和時間依賴性中子學。 (24. Transients, Feedback, and Time-Dependent Neutronics)
 沒有此條件下的單字
沒有此條件下的單字US /ˈkrɪtɪkəl/
・
UK /ˈkrɪtɪkl/
US /məˈtɪriəl/
・
UK /məˈtɪəriəl/
- n. (c./u.)布料;素材;資料;材料;物質
- adj.重要的;物質的
US /ˈpɪriəd/
・
UK /ˈpɪəriəd/
- n. (c./u.)時期;(用於句末;表示斷定的口氣)就這樣;句號;月經;期間
- n. (c./u.)條件;條款;期間;期限;學期;術語;關係;項;妊娠期;任期
- v.t.命名