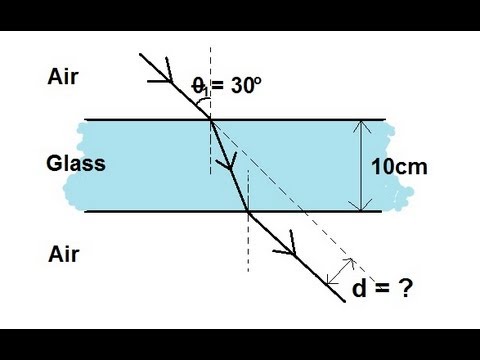
物理 52 折射和斯涅耳定律(11 之 2) 光線穿過玻璃板 (Physics 52 Refraction and Snell's Law (2 of 11) Light Ray Going Through a Glass Slab)
kevin 發佈於 2024 年 10 月 02 日  沒有此條件下的單字
沒有此條件下的單字US /sɪɡˈnɪfɪkənt/
・
UK /sɪgˈnɪfɪkənt/
- v.t./i.出現;估計;我認為〜;認為
- n.身影;(計算過的)數量;肖像;圖;形狀;人物;名人;人影;數字
US /ˈslaɪtli/
・
UK /ˈslaɪtli/
- n.簡述重點;翻新胎面;重述要點;翻新的輪胎
- v.t.概括