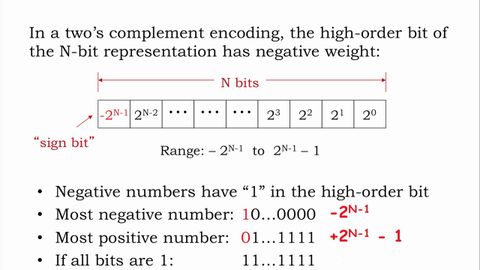
1.2.6 有符號整數:2的補碼 (1.2.6 Signed Integers: 2's complement)
 沒有此條件下的單字
沒有此條件下的單字US /ˌɪndəˈvɪdʒuəl/
・
UK /ˌɪndɪˈvɪdʒuəl/
- n. (c.)個人;單個項目;個體;個人賽
- adj.個人的;獨特的;個別的;獨特的
- v.t./i.出現;估計;我認為〜;認為
- n.身影;(計算過的)數量;肖像;圖;形狀;人物;名人;人影;數字
US /ˈslaɪtli/
・
UK /ˈslaɪtli/
US /tɛkˈnik/
・
UK /tekˈni:k/
- n. (c./u.)技術;工藝;技能;(藝術)技巧