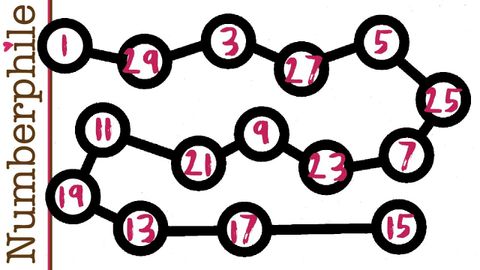
Placeholder Image

字幕列表影片播放

    字幕與單字

    00
    收藏
    影片單字

    struggle

    US /ˈstrʌɡəl/

    ・

    UK /'strʌɡl/

    • v.t./i.奮鬥；掙扎；打鬥；搏鬥
    • n. (c./u.)掙扎；掙扎；奮鬥；難題
    A2 初級初級英檢
    更多
    individual

    US /ˌɪndəˈvɪdʒuəl/

    ・

    UK /ˌɪndɪˈvɪdʒuəl/

    • n. (c.)個人；單個項目；個體；個人賽
    • adj.個人的；獨特的；個別的；獨特的
    A2 初級初級英檢
    更多
    pattern

    US /ˈpætən/

    ・

    UK /'pætn/

    • n. (c./u.)範本；典範；圖案；花樣；模式；方式；規律；紙樣
    • v.t.仿造；用圖案裝飾
    A2 初級多益初級英檢
    更多
    guarantee

    US /ˌɡærənˈti/

    ・

    UK /ˌɡærən'ti:/

    • v.t.保修；保證；保證；法律保障
    • n. (c.)(某產品的)保固；保證某事的如期完成；擔保
    A2 初級多益中級英檢
    更多
    使用能量
    解鎖所有單字
    解鎖發音、解釋及篩選功能
    energy point vocabulary